Dreieck: Besondere Punkte und Linien

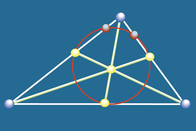
• Der Feuerbachsche Kreis

  Neben den drei Seitenmitten und den drei Höhenfußpunkten liegen bei jedem Dreieck auch die Mittelpunkte zwischen den Ecken und dem Höhenschnittpunkt (die so genannten Euler-Punkte) auf einem Kreis - dem Feuerbachschen Kreis (oder 9-Punkte-Kreis). Spielerisch werden die Zusammenhänge der Mittel ... Detailansicht

  schule-bw.de

• Der Feuerbach-Kreis mit GeoGebra

  Der Feuerbachkreis ist ein besonderer Kreis im Dreieck, der nach Karl Wilhelm Feuerbach benannt ist. Auf ihm liegen neun ausgezeichnete Punkte. Ein GeoGebra-Applet unterstützt die bessere Vorstellung des Feuerbach-Kreises. Detailansicht

  nus.lugsp.at

• Besondere Punkte im Dreieck - Alltägliche Problemstellungen

  Die Schüler/innen werden motiviert, die besonderen Punkte in einem Dreieck anhand alltäglicher Problemstellungen zu erarbeiten und im Anschluss ähnliche Aufgaben zu lösen. Detailansicht

  did.mat.uni-bayreuth.de

• Besondere Punkte des Dreiecks - Lernpfad

  In diesem Lernpfad sollen Schüler und Schülerinnen einer 2. Klasse mit den Begriffen: Höhenschnittpunkt, Umkreismittelpunkt, Inkreismittelpunkt und Schwerpunkt vertraut werden. Die Konstruktion der einzelnen Punkte soll erlernt und die Lage in speziellen Dreiecken beobachtet werden. Am Ende soll ... Detailansicht

  mathe-online.at

• Sechs besondere Punkte auf den Seiten eines Dreiecks

  Altbekannt ist und unzählige Male wiederholt wurde, dass sich die Seitenhalbierenden eines Dreiecks in dessen Schwerpunkt schneiden. Was aber passiert, wenn man die Seitenhälften nochmals halbiert? Welche Bedeutung haben die dabei entstehenden zusätzlichen Teilungspunkte der Dreiecksseiten? Detailansicht

  hjcaspar.de

• Dreiecke - merkwürdige Punkte (Lernpfad)

  Am Beispiel der merkwürdigen Punkte im Dreieck sollen die Schüler/innen mit Hilfe fertiger Applets zur dynamischen Geometrie zum genauen Beobachten und Begründen geführt werden. Experimentierfreudigkeit und selbstentdeckendes Lernen stehen im Vordergrund, wenn bei Veränderung der Dreiecke die La ... Detailansicht

  austromath.at

• Das Dreiecks-Labor

  Je mehr man sich mit dem Thema Dreiecke befasst, desto interessanter wird die Sache. Auch wenn einige der Erkenntnisse über Dreiecke schon mehr als zwei Jahrtausende auf dem Buckel haben: Gerade in den letzten Jahren wurden – oft mit Hilfe von Computern – immer wieder neue, verblüffende Eigensch ... Detailansicht

  walter-fendt.de

• Besondere Linien im Dreieck - Geonet

  Zuerst sollen sich die Schüler/innen die Konstruktionen der Höhen, Winkelhablbierenden, ... eines Dreieckes genau ansehen! Dazu werden die vorhandenen Präsentationen verwendet, die mit Hilfe von Geonet erstellt wurden. Anschließend soll der Schüler/die Schülerin die Konstruktionen nachvollziehe ... Detailansicht

  tiburski.de

• Animationen für die Konstruktion von H, S, U und I

  Hier können Schüler/innen unkompliziert und schnell die einzelnen Konstruktionsschritte mit Hilfe einfacher Animationen nachvollziehen. Es werden auch weiterführende Überlegungen angestellt und genauer erklärt. Detailansicht

  zum.de

• Satz von Wallace (Simson´sche Gerade)

  Legt man von einem Punkt des Umkreises die Lote auf die (Trägergeraden der drei) Dreiecksseiten, dann liegen die drei Fußpunkte stets auf einer Geraden, der Geraden von Wallace (auch "Simson'sche Gerade"). Hier findest du ein Applet zum Satz von Wallace. Detailansicht

  nus.lugsp.at